Day 4 - 08/26/2024

From last class

  • I emailed those who needed partner for their semester project.
  • Quiz: Go to kahoot.it

Linear models

A model is a linear model when the parameters enter linearly.

    1. \(\mu_i = \beta_0 + x_i \beta_1 + x^2_i \beta_2\)
    1. \(\mu_i = \beta_0 + x_{1i} \beta_1 + x_{2i}^{\beta_2}\)
    1. \(\mu_i = \exp(x_{1i}\beta_1 + x_{2i}\beta_2)\)
    1. The famous linear-plus-plateau model: \[\mu_i = \left \{ \begin{aligned} & \beta_0 + x_i \beta_1 && \text{if } x_i \leq x_{crit}\\ & \beta_0 + x_{crit} \beta_1 && \text{if } x_i > x_{crit} \end{aligned} \right.\]

Estimation

  • Continuous versus discrete independent variables.
    • How do we interpret them?

Recall the clover example:

  • 3 clover species planted in pots.
  • 24 plants per species.
  • After 2 months, we harvest and weigh their biomass.
  • We want to estimate how much biomass each genotype produces, eventually know how much and which one produces more.
library(tidyverse)
dd_lotus <- read.csv("data/lotus_part1.csv") %>% 
  transmute(species = factor(species), agb_g) 
summary(dd_lotus)
 species     agb_g      
 A:24    Min.   :1.265  
 C:24    1st Qu.:1.969  
 D:24    Median :2.355  
         Mean   :2.492  
         3rd Qu.:2.936  
         Max.   :4.354  
m1 <- lm(agb_g ~ 0 + species, data = dd_lotus)

By programming m1 <- lm(agb_g ~ 0 + species, data = dd_lotus), we are fitting

\[\mathbf{y} \sim \text{N}(\boldsymbol{\mu}, \sigma^2\mathbf{I}),\] \[\boldsymbol{\mu}=\mathbf{X}\boldsymbol{\beta}.\]

What is another way of writing the model shown here?

Point estimates in \(\boldsymbol{\beta}\)

Let’s calculate \(\hat{\boldsymbol{\beta}}_{LSE} = (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y}\)

X <- model.matrix(m1)
y <- dd_lotus$agb_g
(beta_hat <- solve(t(X)%*%X) %*% t(X)%*%y)
             [,1]
speciesA 2.936576
speciesC 2.396695
speciesD 2.143253
coefficients(m1)
speciesA speciesC speciesD 
2.936576 2.396695 2.143253

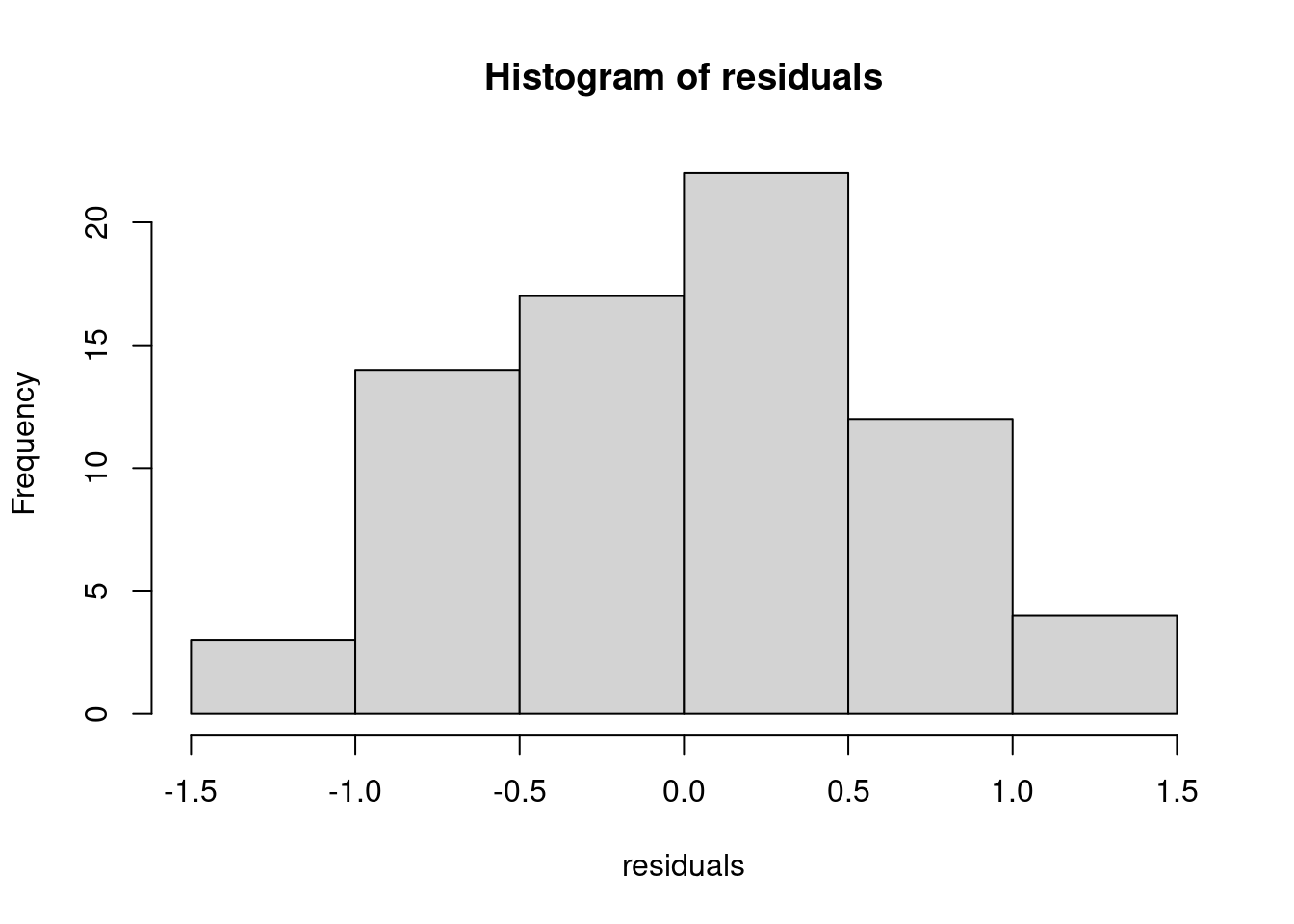
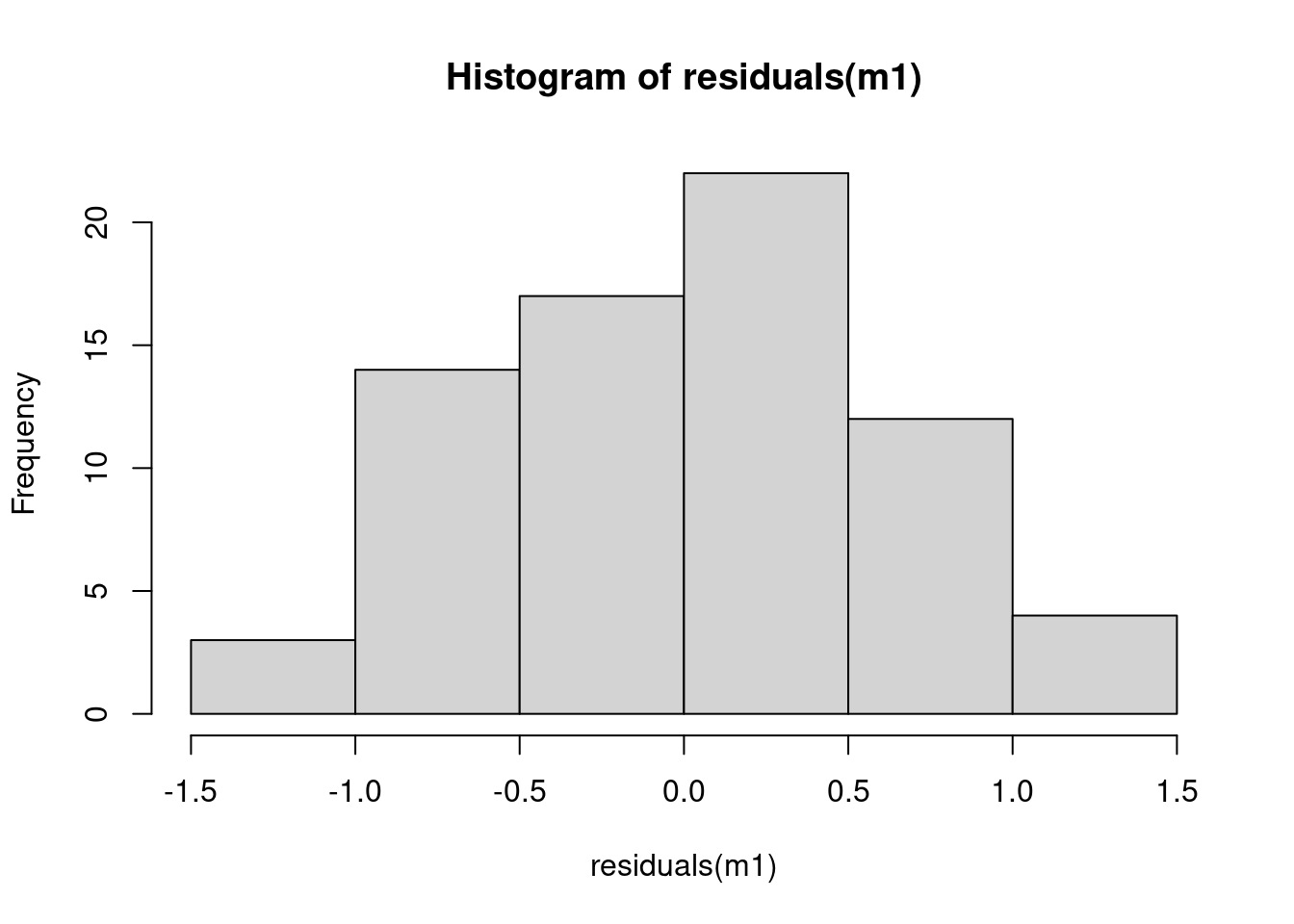
Residuals

head(residuals <- y - X%*%beta_hat)
         [,1]
1 -0.02957583
2 -0.61733583
3 -0.21065583
4  0.47442417
5  1.29108417
6  0.25212417
quantile(residuals)
        0%        25%        50%        75%       100% 
-1.0413558 -0.4618581  0.0325275  0.4484598  1.4173242 
head(residuals(m1))
          1           2           3           4           5           6 
-0.02957583 -0.61733583 -0.21065583  0.47442417  1.29108417  0.25212417 
quantile(residuals(m1))
        0%        25%        50%        75%       100% 
-1.0413558 -0.4618581  0.0325275  0.4484598  1.4173242 
hist(residuals)

hist(residuals(m1))

This will help us for model diagnostics (coming soon!)

Variance \(\sigma^2\)

  • Perhaps one of the most important parameters we will estimate.
  • Prediction accuracy.
  • Prediction intervals, estimation intervals.
  • Degrees of freedom. From \(n-1\) to \(n-p\).

Let’s calculate \(\hat{\sigma}^2 = \frac{\boldsymbol{\hat{\varepsilon}^T\hat{\varepsilon}}}{n-p} = \frac{RSS}{n-p}\)

RSS <- sum(residuals^2)
n <- nrow(dd_lotus)
p <- length(beta_hat)
(sigma2_hat <- RSS/(n-p)) 
[1] 0.3704
(sigma_hat <- sqrt(sigma2_hat))
[1] 0.6086049
summary(m1)$sigma
[1] 0.6086049

Confidence intervals

Confidence intervals are a measure of uncertainty. They are related to other measures of uncertainty, like \(\sigma^2\). We know that \[CI = \hat{\beta} \pm t_{\alpha/2, dfe} \ s.e.,\] where \(t_{\alpha/2, dfe}\) is the t-score that corresponds to the confidence level (i.e., \(\alpha\)) with the degrees of freedom of the error \(\text{rdf}\), and \(s.e.\) is the standard error.

First, let’s calculate the standard error:

unscaled_covariance <- solve(t(X)%*%X)
(se <- sqrt(diag(unscaled_covariance))*sigma_hat)
speciesA speciesC speciesD 
0.124231 0.124231 0.124231 
alpha <- 0.05
dfe <- n-p
(t_score <- qt(p=alpha/2, df = dfe, lower.tail=F))
[1] 1.994945
se*t_score
speciesA speciesC speciesD 
0.247834 0.247834 0.247834 
data.frame(lower = beta_hat - se*t_score, 
           upper = beta_hat + se*t_score)
            lower    upper
speciesA 2.688742 3.184410
speciesC 2.148861 2.644529
speciesD 1.895419 2.391086
confint(m1)
            2.5 %   97.5 %
speciesA 2.688742 3.184410
speciesC 2.148861 2.644529
speciesD 1.895419 2.391086

In summary:

summary(m1)

Call:
lm(formula = agb_g ~ 0 + species, data = dd_lotus)

Residuals:
     Min       1Q   Median       3Q      Max 
-1.04136 -0.46186  0.03253  0.44846  1.41732 

Coefficients:
         Estimate Std. Error t value Pr(>|t|)    
speciesA   2.9366     0.1242   23.64   <2e-16 ***
speciesC   2.3967     0.1242   19.29   <2e-16 ***
speciesD   2.1433     0.1242   17.25   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.6086 on 69 degrees of freedom
Multiple R-squared:  0.9468,    Adjusted R-squared:  0.9445 
F-statistic: 409.5 on 3 and 69 DF,  p-value: < 2.2e-16

For next class

  • No reading!
  • Finish the assignment.
  • Schedule a meeting for the semester project.