url <- "https://raw.githubusercontent.com/jlacasa/stat705_fall2024/main/classes/data/lotus_hw1.csv"
data <- read.csv(url)Day 6 - 08/30/2024
From last class
- Assignments. A few comments:
- Good overall.
geom_smooth()is forbidden from now on! Usestat_function()instead.
- Resubmit next Wednesday.
- How is a statistical model built.
- Deterministic function
- Likelihood function
- Method of estimation
- Good overall.
Linear models revisited
Let’s look at the clover data again.
data %>%
ggplot(aes(doy, stm.length_cm))+
geom_point()+
labs(x = "Day of the year",
y = "Stem length (cm)")+
theme_classic()+
theme(aspect.ratio = 1)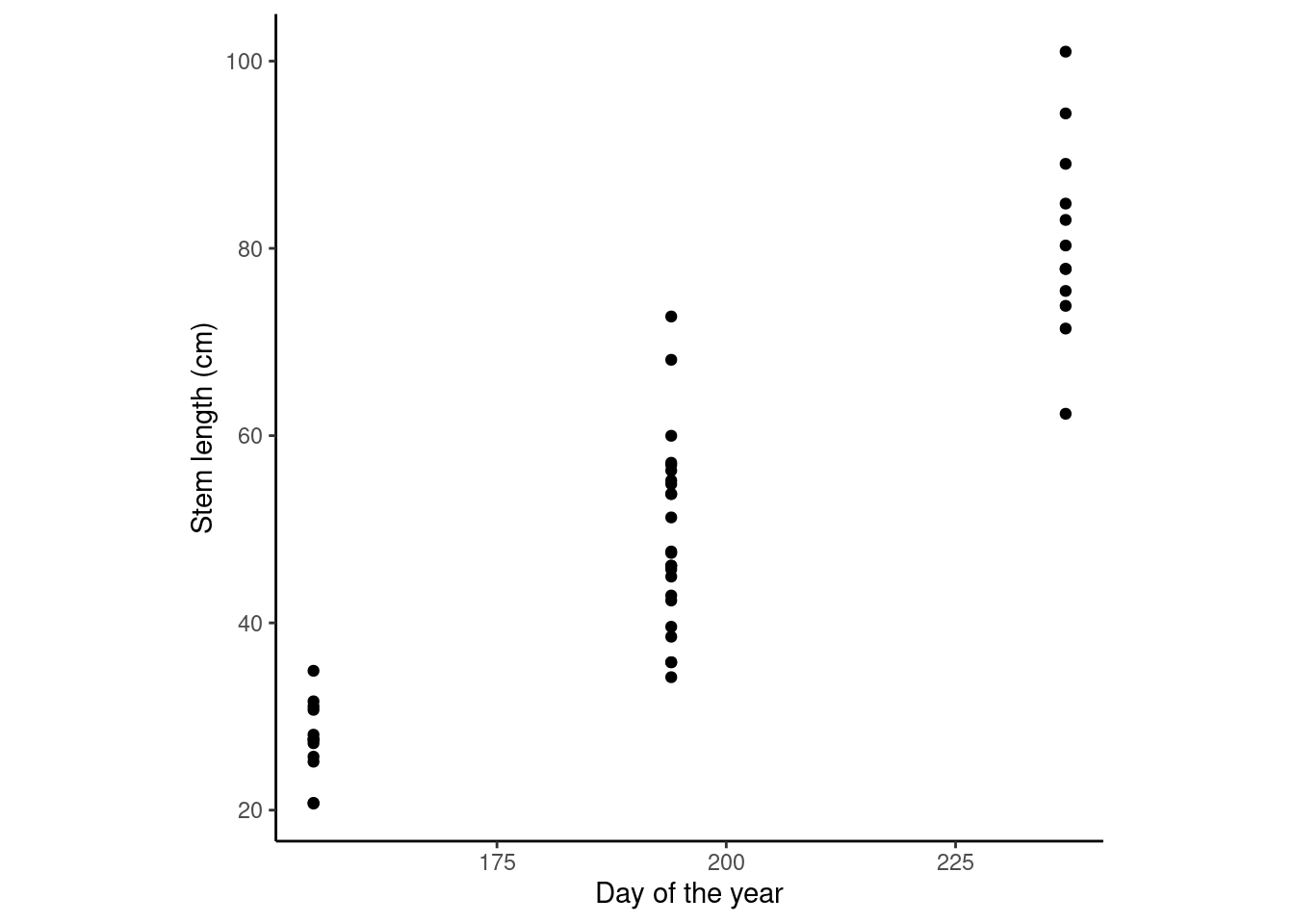
What’s a good model for the data?
One option is \[y_i = \beta_0 + x_i \beta_1 + \varepsilon_i, \] \[\varepsilon_i \sim N(0, \sigma^2),\]
for \(i = 1, 2, ..., n\) (n being the total number of observations), where \(y_i\) is the length of the stem (in cm) of the \(i\)th observation, \(\beta_0\) is the length of the stem (in cm) at day of the year 0 (i.e., December 31 of last year), \(x_i\) is the day of the year of the \(i\)th observation, \(\varepsilon_i\) is the residual of the \(i\)th observation, that is normally distributed.
This is the same as writing
\[\mathbf{y} \sim \text{N}(\boldsymbol{\mu}, \sigma^2\mathbf{I}),\] \[\boldsymbol{\mu}=\mathbf{X}\boldsymbol{\beta}.\]
Estimation
Let’s fit the model written above to data. R script
Confidence intervals
confint(m_cont) 2.5 % 97.5 %
(Intercept) -93.3506731 -57.5098063
doy 0.5618765 0.7436752Some interpretations
The difference in stem length for two consecutive days is between 0.56 and 0.74 with 95% confidence. An additional day growing is associated with and increase in average stem length that is between 0.56 and 0.74 with 95% confidence.[Source (Chapter 3, page 78)].
Also: the interval (0.56, 0.74) contains all the values \(\beta_1^{\star}\) where we would fail to reject the null hypothesis that \(\beta_1 = \beta_1^{\star}\) at level \(\alpha\). [Source].
How much money would you bet on the estimate? Let’s do a simulation.
R code here.
For next class
- No class on Monday.
- Review your assignments.