library(tidyverse)
library(ggpubr)
url <- "https://raw.githubusercontent.com/jlacasa/stat705_fall2024/main/classes/data/lotus_part4.csv"
dd <- read.csv(url)
dd_subset <- dd %>%
filter(trt == "ctrl")Day 15 - 09/23/2024
Analysis of Variance: ANOVA
Helps us answering objectives like finding out “is A different to B or C?”, or “do any of these treatments have an effect on the mean?
Another types of objective (that require other types of modeling tools), for example, would be “to predict y for given levels of A and B” (e.g., predict corn yield with 150 kg N per ha and 20 inches rainfall in the season).
dd %>%
ggplot(aes(species, crown_g))+
geom_boxplot(aes(fill = species))+
scale_fill_manual(values = c("#DB504A", "#43AA8B", "#FAD4C0"))+
labs(x = "Species",
y = "Crown biomass (g)",
fill = "Species")+
theme_classic()+
theme(aspect.ratio = 1)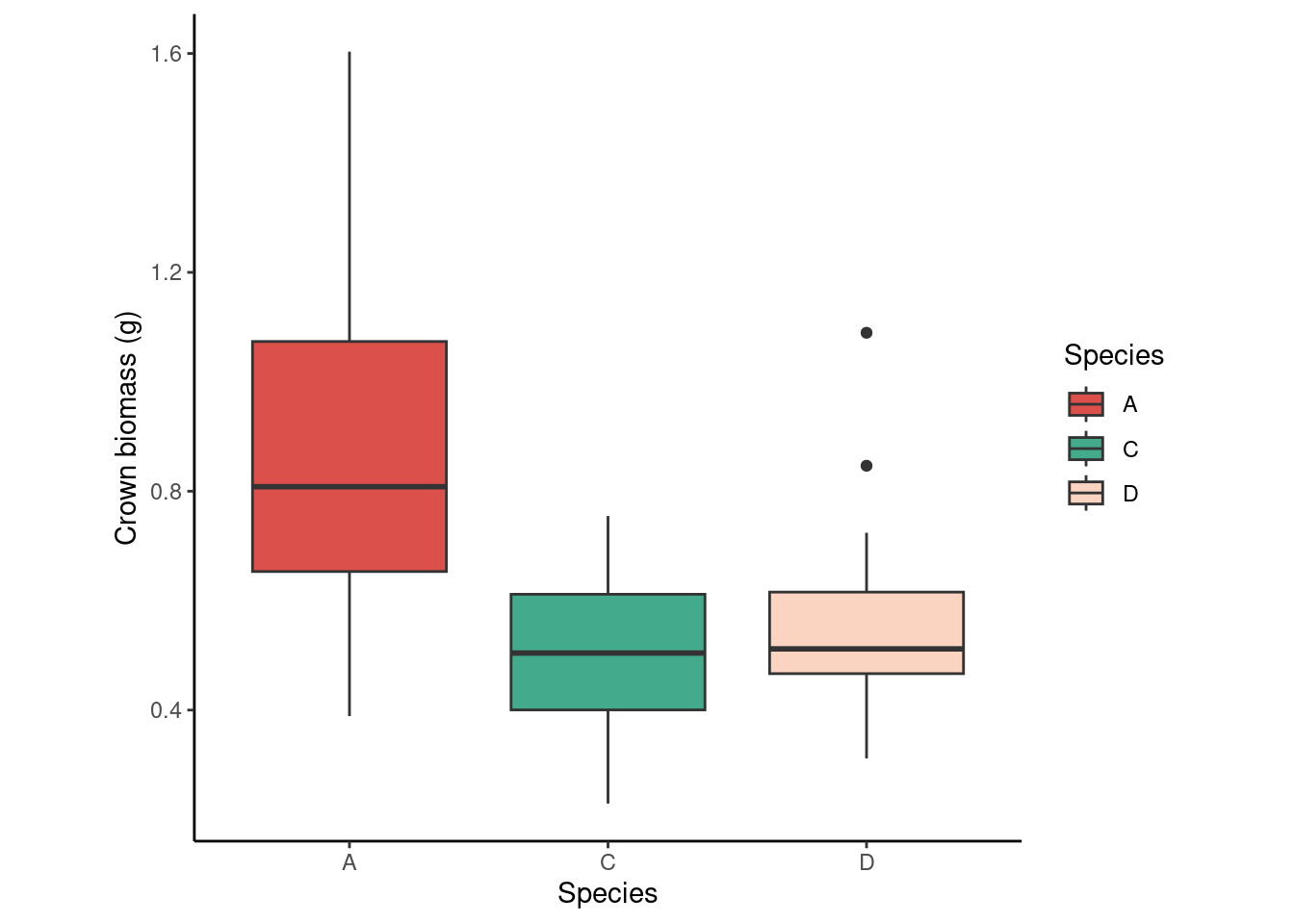
Let’s fit the model \[y_{ij} \sim N(\mu_{ij}, \sigma^2),\]
\[\mu_{ij} = \mu + \beta_{0j},\] where \(y_{ij}\) is the observation of crown biomass for the \(i\)th observation of the \(j\)th species, \(\mu{ij}\) is its mean and \(\sigma^2\) its variance. The means is described with the overall mean \(\mu\) and \(\beta_{0j}\), the effect of the \(j\)th species.
m1 <- lm(crown_g ~ species, data = dd_subset)
summary(m1)
Call:
lm(formula = crown_g ~ species, data = dd_subset)
Residuals:
Min 1Q Median 3Q Max
-0.39175 -0.15785 -0.02829 0.15074 0.63792
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.96540 0.06631 14.560 6.36e-16 ***
speciesC -0.49309 0.09377 -5.259 8.60e-06 ***
speciesD -0.41107 0.09377 -4.384 0.000112 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.2297 on 33 degrees of freedom
Multiple R-squared: 0.4904, Adjusted R-squared: 0.4595
F-statistic: 15.88 on 2 and 33 DF, p-value: 1.477e-05What’s another way of writing out this statistical model?
model.matrix(m1)[1:30,] (Intercept) speciesC speciesD
1 1 0 0
2 1 0 0
3 1 0 0
4 1 0 0
5 1 0 0
6 1 0 0
7 1 0 0
8 1 0 0
9 1 0 0
10 1 0 0
11 1 0 0
12 1 0 0
13 1 1 0
14 1 1 0
15 1 1 0
16 1 1 0
17 1 1 0
18 1 1 0
19 1 1 0
20 1 1 0
21 1 1 0
22 1 1 0
23 1 1 0
24 1 1 0
25 1 0 1
26 1 0 1
27 1 0 1
28 1 0 1
29 1 0 1
30 1 0 1One-way ANOVA
\[H_0: y_{ij} = \mu + \varepsilon_{ij}\] (\(H_0:\) All means are the same regardless of the predictor variable, indicated in subscript \(j\)).
\[H_1: y_{ij} = \mu + \beta_j + \varepsilon_{ij}\] (\(H_1:\) The means are different depending on the predictor variable, indicated in subscript \(j\)).
car::Anova(m1, type = "II")Anova Table (Type II tests)
Response: crown_g
Sum Sq Df F value Pr(>F)
species 1.6754 2 15.878 1.477e-05 ***
Residuals 1.7410 33
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1car::Anova(m1, type = "III")Anova Table (Type III tests)
Response: crown_g
Sum Sq Df F value Pr(>F)
(Intercept) 11.1841 1 211.990 6.360e-16 ***
species 1.6754 2 15.878 1.477e-05 ***
Residuals 1.7410 33
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- Self-study questions:
- If the treatment factor has two levels, what is the difference between a t-test and an ANOVA test?
- Can you know which mean is larger based on the ANOVA results?
Two-way ANOVA
Used to answer the same types of questions, this analysis is most common in factorial designs.
dd %>%
ggplot(aes(species, crown_g))+
geom_boxplot(aes(fill = trt, color = species))+
scale_fill_manual(values = c("white", "#F7B05B"))+
scale_color_manual(values = c("#DB504A", "#43AA8B", "#FAD4C0"))+
labs(x = "Species",
y = "Crown biomass (g)",
fill = "Treatment",
color = "Species")+
theme_classic()+
theme(aspect.ratio = 1)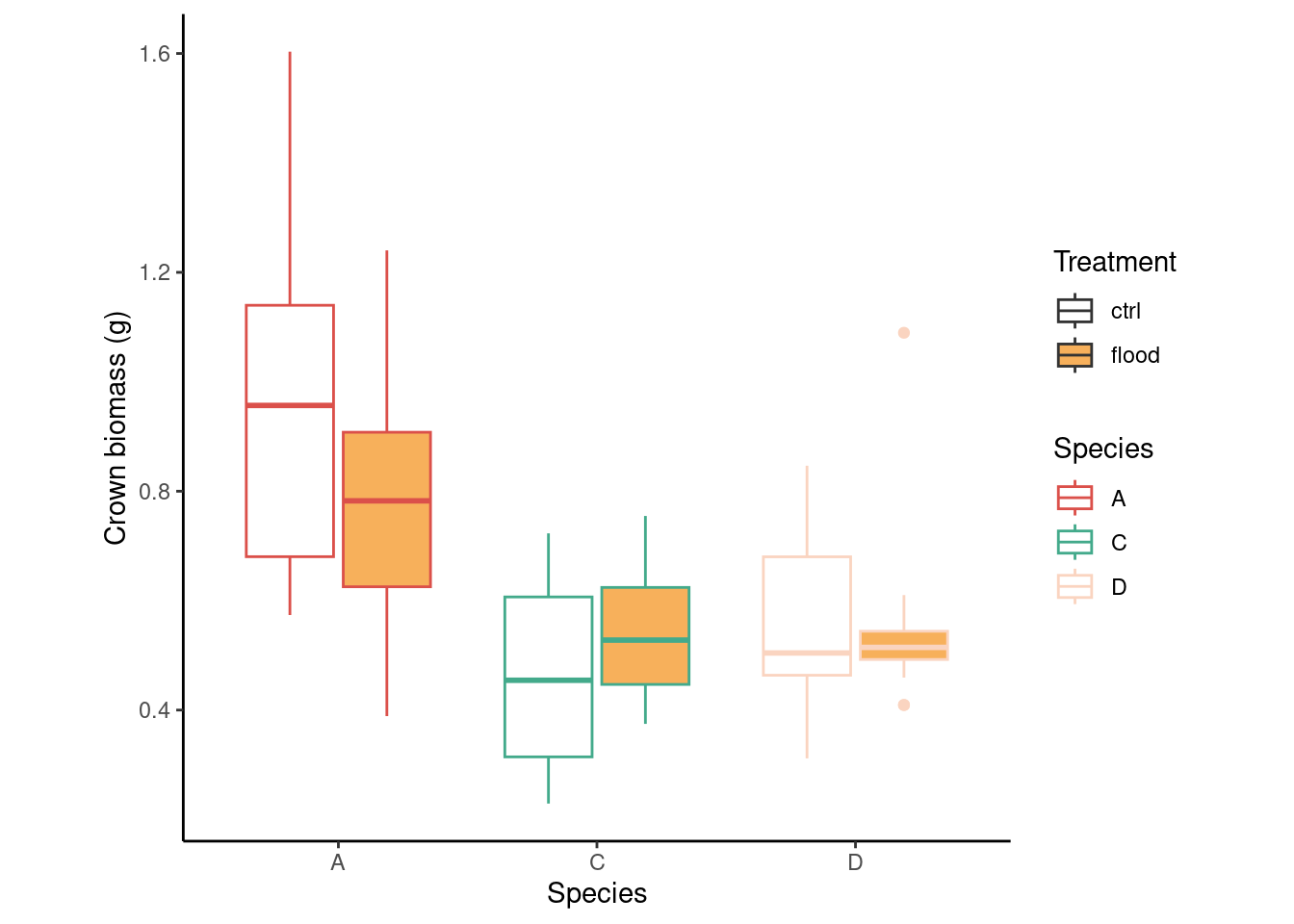
m2 <- lm(crown_g ~ species*trt, data = dd)
summary(m2)
Call:
lm(formula = crown_g ~ species * trt, data = dd)
Residuals:
Min 1Q Median 3Q Max
-0.39578 -0.12946 -0.02559 0.12274 0.63791
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.96541 0.06040 15.984 < 2e-16 ***
speciesC -0.49310 0.08541 -5.773 2.28e-07 ***
speciesD -0.41107 0.08541 -4.813 9.03e-06 ***
trtflood -0.18065 0.08541 -2.115 0.0382 *
speciesC:trtflood 0.24622 0.12079 2.038 0.0455 *
speciesD:trtflood 0.17967 0.12079 1.487 0.1417
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.2092 on 66 degrees of freedom
Multiple R-squared: 0.4279, Adjusted R-squared: 0.3846
F-statistic: 9.875 on 5 and 66 DF, p-value: 4.427e-07model.matrix(m2)[1:30,] (Intercept) speciesC speciesD trtflood speciesC:trtflood speciesD:trtflood
1 1 0 0 0 0 0
2 1 0 0 0 0 0
3 1 0 0 0 0 0
4 1 0 0 0 0 0
5 1 0 0 0 0 0
6 1 0 0 0 0 0
7 1 0 0 0 0 0
8 1 0 0 0 0 0
9 1 0 0 0 0 0
10 1 0 0 0 0 0
11 1 0 0 0 0 0
12 1 0 0 0 0 0
13 1 1 0 0 0 0
14 1 1 0 0 0 0
15 1 1 0 0 0 0
16 1 1 0 0 0 0
17 1 1 0 0 0 0
18 1 1 0 0 0 0
19 1 1 0 0 0 0
20 1 1 0 0 0 0
21 1 1 0 0 0 0
22 1 1 0 0 0 0
23 1 1 0 0 0 0
24 1 1 0 0 0 0
25 1 0 1 0 0 0
26 1 0 1 0 0 0
27 1 0 1 0 0 0
28 1 0 1 0 0 0
29 1 0 1 0 0 0
30 1 0 1 0 0 0car::Anova(m2, type = "II")Anova Table (Type II tests)
Response: crown_g
Sum Sq Df F value Pr(>F)
species 1.93969 2 22.1558 4.35e-08 ***
trt 0.02694 1 0.6154 0.4356
species:trt 0.19466 2 2.2235 0.1163
Residuals 2.88908 66
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1car::Anova(m2, type = "III")Anova Table (Type III tests)
Response: crown_g
Sum Sq Df F value Pr(>F)
(Intercept) 11.1841 1 255.4967 < 2.2e-16 ***
species 1.6754 2 19.1370 2.787e-07 ***
trt 0.1958 1 4.4729 0.03822 *
species:trt 0.1947 2 2.2235 0.11628
Residuals 2.8891 66
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Using a combination of categorical (indicator) variables and continuous variables
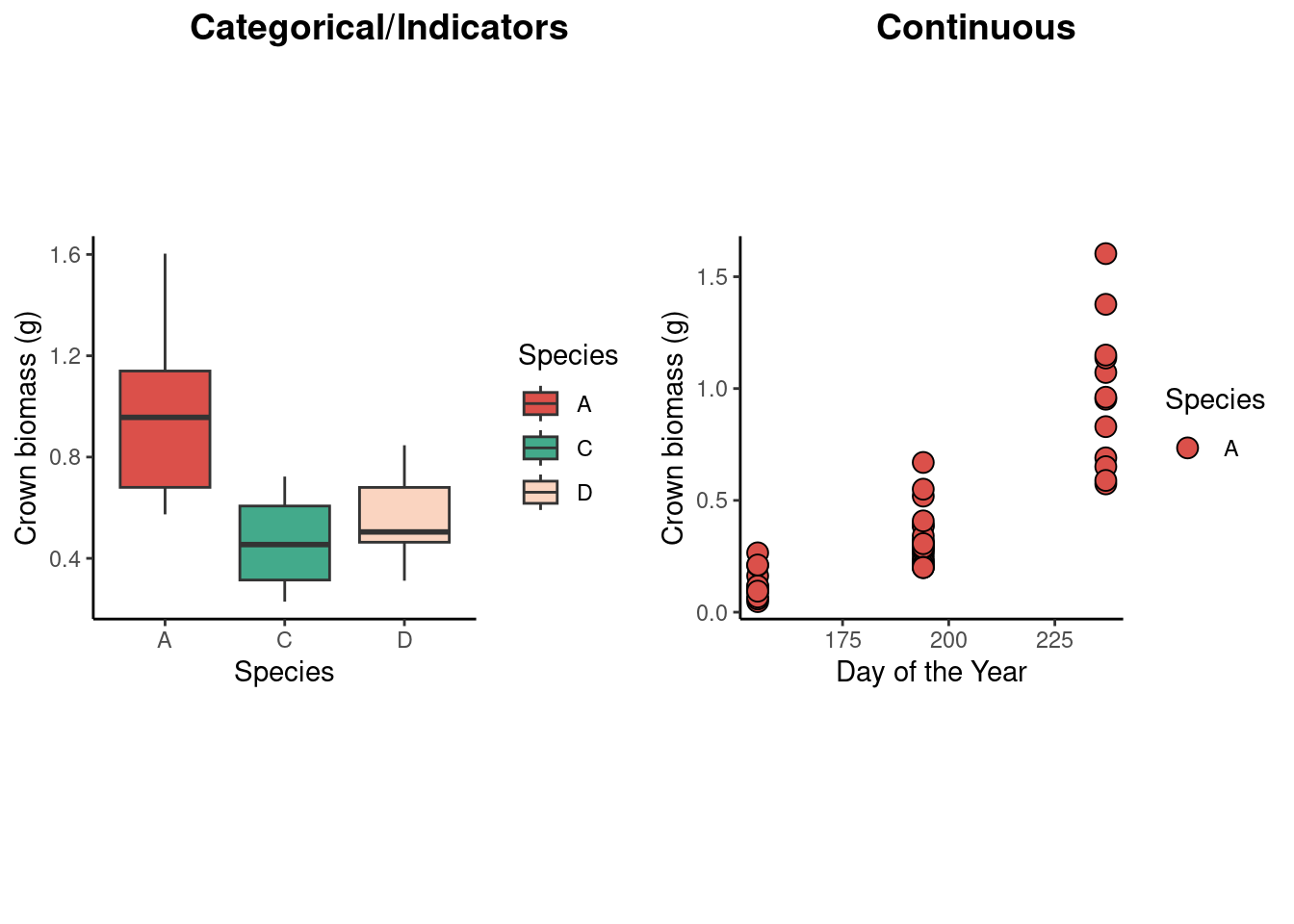
Review types of explanatory data
url2 <- "https://raw.githubusercontent.com/jlacasa/stat705_fall2024/main/classes/data/lotus_part3.csv"
dd2 <- read.csv(url2)
ggarrange(
dd2 %>%
filter(doy ==237) %>%
ggplot(aes(species, crown_g))+
geom_boxplot(aes(fill = species))+
scale_fill_manual(values = c("#DB504A", "#43AA8B", "#FAD4C0"))+
labs(x = "Species",
y = "Crown biomass (g)",
fill = "Species")+
theme_classic()+
theme(aspect.ratio = 1),
dd2 %>%
filter(species== "A") %>%
ggplot(aes(doy, crown_g))+
geom_point(aes(fill = species), shape = 21, size =3.5)+
scale_fill_manual(values = c("#DB504A", "#43AA8B", "#FAD4C0"))+
labs(x = "Day of the Year",
y = "Crown biomass (g)",
fill = "Species")+
theme_classic()+
theme(aspect.ratio = 1),
ncol =2,
labels = c("Categorical/Indicators", "Continuous"),
label.x = c(0, 0.2)
)
dd2 %>%
ggplot(aes(doy, crown_g))+
geom_point(aes(fill = species), shape = 21, size =3.5)+
scale_fill_manual(values = c("#DB504A", "#43AA8B", "#FAD4C0"))+
labs(x = "Day of the Year",
y = "Crown biomass (g)",
fill = "Species")+
theme_classic()+
theme(aspect.ratio = 1)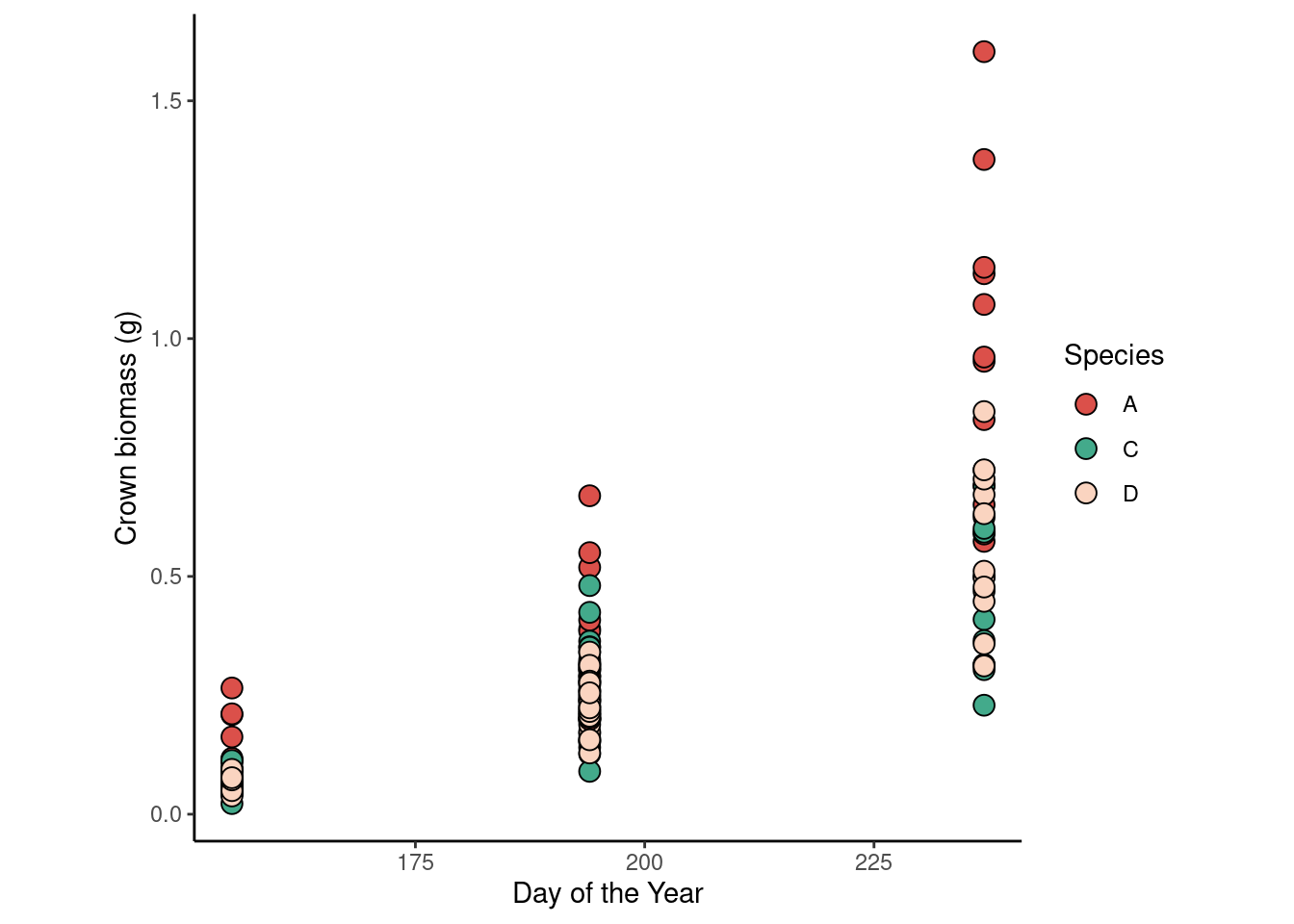
m3 <- lm(crown_g ~ species*doy, data = dd2)
summary(m3)
Call:
lm(formula = crown_g ~ species * doy, data = dd2)
Residuals:
Min 1Q Median 3Q Max
-0.29416 -0.09688 -0.00858 0.06046 0.73550
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.5809069 0.1438577 -10.989 < 2e-16 ***
speciesC 0.8764868 0.2034455 4.308 3.11e-05 ***
speciesD 0.6864100 0.2034455 3.374 0.000962 ***
doy 0.0103322 0.0007297 14.159 < 2e-16 ***
speciesC:doy -0.0054042 0.0010320 -5.237 5.96e-07 ***
speciesD:doy -0.0043320 0.0010320 -4.198 4.80e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.1467 on 138 degrees of freedom
Multiple R-squared: 0.7207, Adjusted R-squared: 0.7105
F-statistic: 71.21 on 5 and 138 DF, p-value: < 2.2e-16car::Anova(m3, type = "III")Anova Table (Type III tests)
Response: crown_g
Sum Sq Df F value Pr(>F)
(Intercept) 2.5974 1 120.766 < 2.2e-16 ***
species 0.4419 2 10.272 6.937e-05 ***
doy 4.3120 1 200.491 < 2.2e-16 ***
species:doy 0.6614 2 15.376 9.368e-07 ***
Residuals 2.9680 138
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1model.matrix(m3)[1:30,] (Intercept) speciesC speciesD doy speciesC:doy speciesD:doy
1 1 0 0 155 0 0
2 1 0 0 155 0 0
3 1 0 0 155 0 0
4 1 0 0 155 0 0
5 1 0 0 155 0 0
6 1 0 0 155 0 0
7 1 0 0 155 0 0
8 1 0 0 155 0 0
9 1 0 0 155 0 0
10 1 0 0 155 0 0
11 1 0 0 155 0 0
12 1 0 0 155 0 0
13 1 1 0 155 155 0
14 1 1 0 155 155 0
15 1 1 0 155 155 0
16 1 1 0 155 155 0
17 1 1 0 155 155 0
18 1 1 0 155 155 0
19 1 1 0 155 155 0
20 1 1 0 155 155 0
21 1 1 0 155 155 0
22 1 1 0 155 155 0
23 1 1 0 155 155 0
24 1 1 0 155 155 0
25 1 0 1 155 0 155
26 1 0 1 155 0 155
27 1 0 1 155 0 155
28 1 0 1 155 0 155
29 1 0 1 155 0 155
30 1 0 1 155 0 155Let’s put this in context
- Don’t forget our assumptions:
- residuals are iid \(\sim N(0, \sigma^2)\)
- parameters enter linearly (linear model)
- homoscedasticity (i.e., constant variance)
- residuals are iid \(\sim N(0, \sigma^2)\)
- Whiteboard. Context in data analysis workflow.
For next class
- Read Chapter 15.
- Resubmit Assignment 2.
- Following: model diagnostics, model selection.